Tri the Illini swim analysis

On Saturday I participated in the Tri the Illini triathlon on the University of Illinois campus. You can read all about the race here. One of the interesting things about this race is that participants were started 10 seconds apart in order of their estimated time for the 300 meter swim in the indoor pool. In theory, if everyone swims at their estimated time nobody will have to pass anyone else in the pool. Now that the results have been posted, let's take a quick look to see how accurate the participants' predictions were.

Import the data from the results web page.

data = Import["http://www.mattoonmultisport.com/images/stories/results/trithetri/overall.htm", {"HTML", "FullData"}];

Clean it up a bit by removing empty elements, labels, and column headers. Basically, we only want the entries with an integer value in the first column (the overall place).

Length[data]

9

data = DeleteCases[data, {}|{{}}];

Length[data]

1

data = First[data];

Length[data]

345

Take[data, 12]//InputForm

{{"", "------- Swim -------", "------- T1 -------",
"------- Bike -------", "------- T2 -------", "------- Run -------",
"Total"}, {"Place", "Name", "Bib No", "Age", "Rnk", "Time", "Pace",
"Rnk", "Time", "Pace", "Rnk", "Time", "Rate", "Rnk", "Time", "Pace",
"Rnk", "Time", "Pace", "Time"}, {1, "Daniel Bretscher", 8, 26, 3,
"04:19.75", "23:59/M", 1, "00:34.00", "", 1, "26:42.95", "24.7mph",
19, "00:44.25", "", 2, "16:09.15", "5:23/M", "48:30.10"},
{2, "Michael Bridenbaug", 27, 25, 15, "04:39.50", "25:50/M", 6,
"00:43.65", "", 5, "28:16.55", "23.3mph", 6, "00:37.55", "", 4,
"16:15.75", "5:25/M", "50:33.00"}, {3, "Peter Garde", 17, 24, 24,
"04:53.05", "27:08/M", 51, "01:21.90", "", 2, "27:06.50", "24.4mph",
109, "01:05.95", "", 3, "16:13.05", "5:24/M", "50:40.45"},
{4, "Nickolaus Early", 16, 29, 2, "04:07.30", "22:52/M", 18,
"00:57.45", "", 4, "27:58.40", "23.6mph", 4, "00:36.40", "", 9,
"18:01.25", "6:00/M", "51:40.80"}, {5, "Zach Rosenbarger", 78, 33, 50,
"05:15.85", "29:10/M", 45, "01:16.75", "", 3, "27:42.00", "23.8mph",
54, "00:53.30", "", 5, "17:11.80", "5:44/M", "52:19.70"},
{6, "Edward Elliot", 32, 28, 11, "04:35.45", "25:28/M", 16, "00:56.15",
"", 6, "28:23.40", "23.3mph", 38, "00:48.85", "", 7, "17:43.75",
"5:54/M", "52:27.60"}, {7, "Ryan Forster", 28, 27, 35, "05:03.95",
"28:03/M", 9, "00:46.20", "", 12, "29:39.95", "22.3mph", 39,
"00:49.05", "", 11, "18:07.00", "6:02/M", "54:26.15"},
{8, "Jun Yamaguchi", 15, 27, 27, "04:58.20", "27:36/M", 2, "00:37.85",
"", 11, "29:36.70", "22.3mph", 30, "00:47.05", "", 13, "18:49.30",
"6:16/M", "54:49.10"}, {9, "Scott Paluska", 63, 42, 71, "05:35.30",
"31:01/M", 3, "00:40.70", "", 7, "28:44.00", "23.0mph", 118,
"01:06.90", "", 12, "18:43.60", "6:14/M", "54:50.50"},
{10, "Rob Raguet-Schoofield", 42, 31, 44, "05:09.75", "28:37/M", 20,
"01:01.55", "", 18, "30:10.50", "21.9mph", 45, "00:51.45", "", 8,
"17:52.60", "5:57/M", "55:05.85"}}

data = DeleteCases[data, x_/;Head[First[x]] === String];

Length[data]

301

places = data[[All, 1]];

places==Range[301]

True

swimSeeds = data[[All, 3]];

swimPlaces = data[[All, 5]];

swimΔ = swimPlaces - swimSeeds;

Take a look at {overall place, swim seed, swim place, swim Δ} for each participant. A negative Δ means the participant's swim place was better than their seeded swim place, while a positive Δ means the participant's swim place was worse than their seeded swim place.

Grid[Prepend[Transpose[{places, swimSeeds, swimPlaces, swimΔ}], {"Overall\nPlace", "Swim\nSeed", "Swim\nPlace", "Swim\nΔ"}], Dividers->All]

Overall Place	Swim Seed	Swim Place	Swim Δ
1	8	3	- 5
2	27	15	- 12
3	17	24	7
4	16	2	- 14
5	78	50	- 28
6	32	11	- 21
7	28	35	7
8	15	27	12
9	63	71	8
10	42	44	2
11	9	9	0
12	62	31	- 31
13	54	105	51
14	30	14	- 16
15	200	155	- 45
16	14	8	- 6
17	83	83	0
18	6	33	27
19	47	53	6
20	66	34	- 32
21	40	102	62
22	86	106	20
23	100	75	- 25
24	45	59	14
25	120	58	- 62
26	4	12	8
27	3	36	33
28	33	13	- 20
29	51	25	- 26
30	72	115	43
31	12	16	4
32	39	7	- 32
33	65	66	1
34	330	240	- 90
35	48	64	16
36	21	6	- 15
37	13	5	- 8
38	68	56	- 12
39	212	89	- 123
40	214	79	- 135
41	67	45	- 22
42	76	21	- 55
43	75	211	136
44	81	63	- 18
45	251	172	- 79
46	44	114	70
47	162	95	- 67
48	7	4	- 3
49	74	92	18
50	55	48	- 7
51	52	29	- 23
52	237	124	- 113
53	11	18	7
54	77	98	21
55	56	30	- 26
56	117	104	- 13
57	1	1	0
58	300	74	- 226
59	151	125	- 26
60	139	82	- 57
61	274	151	- 123
62	64	22	- 42
63	122	87	- 35
64	36	37	1
65	250	243	- 7
66	154	148	- 6
67	121	90	- 31
68	136	258	122
69	282	146	- 136
70	87	69	- 18
71	112	110	- 2
72	315	278	- 37
73	24	19	- 5
74	80	77	- 3
75	135	184	49
76	69	97	28
77	185	163	- 22
78	59	49	- 10
79	128	94	- 34
80	60	51	- 9
81	187	28	- 159
82	35	20	- 15
83	113	134	21
84	90	40	- 50
85	163	17	- 146
86	22	38	16
87	133	200	67
88	267	73	- 194
89	256	145	- 111
90	92	122	30
91	159	206	47
92	165	130	- 35
93	137	153	16
94	149	128	- 21
95	104	80	- 24
96	182	136	- 46
97	26	46	20
98	172	93	- 79
99	241	55	- 186
100	277	109	- 168
101	114	165	51
102	97	103	6
103	131	159	28
104	228	194	- 34
105	46	117	71
106	141	199	58
107	132	162	30
108	246	132	- 114
109	115	205	90
110	213	183	- 30
111	127	181	54
112	157	147	- 10
113	254	131	- 123
114	266	256	- 10
115	41	61	20
116	61	39	- 22
117	43	41	- 2
118	191	196	5
119	106	257	151
120	96	81	- 15
121	234	60	- 174
122	201	85	- 116
123	108	142	34
124	161	218	57
125	123	149	26
126	98	150	52
127	138	271	133
128	265	179	- 86
129	195	54	- 141
130	50	86	36
131	53	161	108
132	170	137	- 33
133	58	26	- 32
134	169	120	- 49
135	204	249	45
136	342	65	- 277
137	91	100	9
138	103	47	- 56
139	125	182	57
140	82	68	- 14
141	88	76	- 12
142	147	241	94
143	238	107	- 131
144	303	202	- 101
145	70	191	121
146	297	247	- 50
147	188	178	- 10
148	2	10	8
149	130	164	34
150	311	288	- 23
151	168	187	19
152	283	158	- 125
153	144	216	72
154	295	287	- 8
155	208	244	36
156	287	157	- 130
157	111	176	65
158	199	111	- 88
159	272	223	- 49
160	179	242	63
161	84	190	106
162	310	152	- 158
163	109	118	9
164	37	67	30
165	180	227	47
166	340	135	- 205
167	328	193	- 135
168	263	197	- 66
169	312	250	- 62
170	148	143	- 5
171	242	224	- 18
172	278	230	- 48
173	253	139	- 114
174	292	279	- 13
175	10	32	22
176	276	254	- 22
177	18	101	83
178	155	167	12
179	271	276	5
180	102	169	67
181	192	248	56
182	257	78	- 179
183	93	210	117
184	346	294	- 52
185	255	269	14
186	158	192	34
187	49	171	122
188	126	201	75
189	143	140	- 3
190	231	88	- 143
191	220	186	- 34
192	298	177	- 121
193	107	144	37
194	94	129	35
195	129	188	59
196	184	274	90
197	116	273	157
198	224	259	35
199	186	214	28
200	174	198	24
201	290	221	- 69
202	95	175	80
203	152	215	63
204	189	246	57
205	156	239	83
206	336	141	- 195
207	118	174	56
208	197	91	- 106
209	194	280	86
210	196	212	16
211	291	121	- 170
212	190	189	- 1
213	247	119	- 128
214	286	126	- 160
215	219	52	- 167
216	229	170	- 59
217	23	23	0
218	236	277	41
219	235	265	30
220	252	204	- 48
221	258	281	23
222	99	84	- 15
223	211	226	15
224	279	272	- 7
225	216	267	51
226	167	116	- 51
227	243	275	32
228	262	220	- 42
229	230	154	- 76
230	288	166	- 122
231	337	251	- 86
232	269	228	- 41
233	233	252	19
234	20	208	188
235	110	185	75
236	308	284	- 24
237	261	231	- 30
238	245	127	- 118
239	343	283	- 60
240	160	70	- 90
241	150	264	114
242	85	156	71
243	5	173	168
244	347	213	- 134
245	153	203	50
246	175	219	44
247	339	298	- 41
248	134	290	156
249	203	42	- 161
250	348	282	- 66
251	289	112	- 177
252	124	168	44
253	218	238	20
254	145	207	62
255	119	113	- 6
256	183	123	- 60
257	299	236	- 63
258	73	62	- 11
259	302	261	- 41
260	29	96	67
261	57	57	0
262	173	225	52
263	281	255	- 26
264	31	99	68
265	275	270	- 5
266	319	296	- 23
267	181	245	64
268	178	301	123
269	89	108	19
270	307	291	- 16
271	294	229	- 65
272	215	43	- 172
273	176	160	- 16
274	270	180	- 90
275	240	195	- 45
276	217	263	46
277	318	302	- 16
278	316	303	- 13
279	285	237	- 48
280	280	297	17
281	177	72	- 105
282	207	234	27
283	314	217	- 97
284	309	232	- 77
285	306	253	- 53
286	248	292	44
287	193	289	96
288	296	286	- 10
289	227	285	58
290	171	222	51
291	345	304	- 41
292	305	262	- 43
293	71	268	197
294	264	266	2
295	226	235	9
296	225	209	- 16
297	273	295	22
298	244	260	16
299	142	305	163
300	209	306	97
301	313	307	- 6

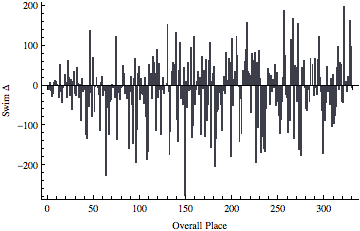
It looks like the race leaders were fairly accurate in their predictions, while the differences start to become greater around 40th place or so.

BarChart[swimΔ, FrameLabel->{"Overall Place", "Swim Δ"}, Frame->{True, True, False, False}]

From the sorted Δs it looks like about half of the participants were within 50 places or so of their seeds, while a few were way off (in both directions).

BarChart[Sort[swimΔ]]

Median[Abs@swimΔ]

41

N[Mean[Abs@swimΔ]]

56.70099667774086`

N[StandardDeviation[Abs@swimΔ]]

51.80100030247153`

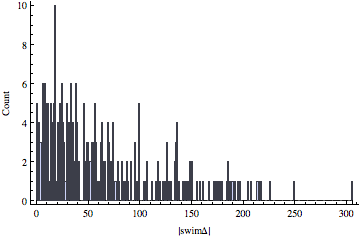
Commonest[Abs@swimΔ]

{16}

tally = Sort[Tally[Abs@swimΔ]]

{{0, 5}, {1, 3}, {2, 4}, {3, 3}, {4, 1}, {5, 6}, {6, 6}, {7, 6}, {8, 5}, {9, 4}, {10, 5}, {11, 1}, {12, 5}, {13, 3}, {14, 4}, {15, 5}, {16, 10}, {17, 1}, {18, 4}, {19, 3}, {20, 5}, {21, 4}, {22, 6}, {23, 4}, {24, 3}, {25, 1}, {26, 5}, {27, 2}, {28, 4}, {30, 6}, {31, 2}, {32, 4}, {33, 2}, {34, 6}, {35, 4}, {36, 2}, {37, 2}, {41, 5}, {42, 2}, {43, 2}, {44, 3}, {45, 3}, {46, 2}, {47, 2}, {48, 3}, {49, 3}, {50, 3}, {51, 5}, {52, 3}, {53, 1}, {54, 1}, {55, 1}, {56, 3}, {57, 4}, {58, 2}, {59, 2}, {60, 2}, {62, 4}, {63, 3}, {64, 1}, {65, 2}, {66, 2}, {67, 4}, {68, 1}, {69, 1}, {70, 1}, {71, 2}, {72, 1}, {75, 2}, {76, 1}, {77, 1}, {79, 2}, {80, 1}, {83, 2}, {86, 3}, {88, 1}, {90, 5}, {94, 1}, {96, 1}, {97, 2}, {101, 1}, {105, 1}, {106, 2}, {108, 1}, {111, 1}, {113, 1}, {114, 3}, {116, 1}, {117, 1}, {118, 1}, {121, 2}, {122, 3}, {123, 4}, {125, 1}, {128, 1}, {130, 1}, {131, 1}, {133, 1}, {134, 1}, {135, 2}, {136, 2}, {141, 1}, {143, 1}, {146, 1}, {151, 1}, {156, 1}, {157, 1}, {158, 1}, {159, 1}, {160, 1}, {161, 1}, {163, 1}, {167, 1}, {168, 2}, {170, 1}, {172, 1}, {174, 1}, {177, 1}, {179, 1}, {186, 1}, {188, 1}, {194, 1}, {195, 1}, {197, 1}, {205, 1}, {226, 1}, {277, 1}}

BarChart[Range[0, Max[tally[[All, 1]]]]/.Append[Apply[Rule, tally, 1], _Integer->0], FrameLabel->{TraditionalForm[Abs["swimΔ"]], "Count"}, Frame->{True, True, False, False}]

It looks like most people were 40-50 places off (in one direction or the other) from their seed. This is higher than I would have expected. The most common difference was 16 places. There must have been a lot of passing going on.

Download Mathematica Notebook