[localhost:~]$ cat * > /dev/ragfield

Thursday, May 21, 2009

Twitter usage patterns

What kind of Twitterer am I? I'm kind of on a role with this data mining of Twitter so I'll take a brief look at my own Twitter habits.
<<Twitter`
session = TwitterSessionOpen["User"->"ragfield"]
TwitterSession[<ragfield>]
Length[tweets = TwitterUserAllTimeline[session]]
1487
DateDifference[TwitterStatusDate@Last@tweets, TwitterStatusDate@First@tweets, {"Year", "Month", "Day"}]
{{1, Year}, {3, Month}, {20.83855324074074`, Day}}
Length[tweets] / DateDifference[TwitterStatusDate@Last@tweets, TwitterStatusDate@First@tweets, {"Day"}][[1, 1]]
3.125009501379522`
1487 total tweets in the last 1 year, 3 months, and 21 days. On average that's 3.125 tweets per day.
DateListPlot[Tally[{#[[1]], #[[2]], 1, 0, 0, 0.}&/@(TwitterStatusDate/@tweets)], Joined->True, Filling->Axis, FrameLabel->{"Month", "Tweets per month"}, PlotLabel->"Ragfield Twitter usage", DateTicksFormat->{"MonthNameShort", " ", "Year"}]
Ragfield Twitter usage
Total[StringLength[TwitterStatusText[#]]&/@tweets]
107442
N[% / Length[tweets]]
72.2542030934768`
107,442 total characters typed. On average that's 72 characters per tweet, roughly half the allotted space.
First@SortBy[TwitterStatusText/@tweets, StringLength]
bed
My shortest tweet was simply "bed".
Length[allWords = StringSplit[StringJoin[Riffle[TwitterStatusText/@tweets, " "]], Except[WordCharacter|"'"]..]]
19188
19,188 unique words typed.
Length[allWords = DeleteCases[allWords, x_/;StringMatchQ[x, DigitCharacter..]]]
18528
18,528 if you don't count numbers.
First@Reverse@SortBy[Tally[allWords], Part[#, 2]&]
{the, 604}
The most common word I've typed is "the". That's not terribly useful. Let's take a look at just nouns to see what kind of topics I mention most frequently.
Length[nouns = Cases[allWords, x_/;MemberQ[WordData[x], "Noun", ‚àû]]]
7883
Grid[Take[Reverse@SortBy[Tally[nouns], Part[#, 2]&], 30], Alignment->{{Right, Left}}]
I431
a419
in259
at126
have77
bike62
work54
time52
out51
are48
ride45
think43
so43
run43
now42
like42
one38
d38
morning36
last36
can36
race35
miles35
mile35
home35
first35
way34
still34
year31
good31
Most common topics: bike, work, time, ride, think, run, like, morning, race, mile(s), home.
We can do the same thing with verbs to see what kind of actions I describe most frequently.
Length[verbs = Cases[allWords, x_/;MemberQ[WordData[x], "Verb", ‚àû]]]
4300
Grid[Take[Reverse@SortBy[Tally[verbs], Part[#, 2]&], 30], Alignment->{{Right, Left}}]
is164
was108
be80
have77
bike62
up59
work54
time52
out51
ride45
been44
think43
run43
has43
like42
last36
can36
race35
home35
still34
had32
got32
get30
do30
back28
long27
will26
see26
did25
know24
Most common actions: bike, work, ride, think, run, race, see, know. I guess there's a lot of overlap between the nouns and the verbs.
It's also pretty easy to determine the other users I mention most frequently.
Grid[Take[Reverse@SortBy[Tally[StringCases[StringJoin[Riffle[TwitterStatusText/@tweets, " "]], "@"~~a:Except[WhitespaceCharacter]..:>Hyperlink[ToLowerCase[a], "http://twitter.com/"<>ToLowerCase[a]]]], Part[#, 2]&], 10]]
melissa_raguet84
spoonshake69
esmithrunner32
erik_d28
dbfulton18
gutzville14
ultrashea11
erik__d9
adamengst9
chockenberry6
Downloads
Download Twitter.m.
Download WebUtils.m (required by Twitter.m).
Download Mathematica Notebook.
Posted by at 1 comment:
Labels: , , ,

Wednesday, May 20, 2009

Wolfram|Alpha tweet analysis

Last month I wrote about my Twitter package for Mathematica. Shortly thereafter I wrote a similar post for my company's blog. That post seems to have been well received and has generated quite a bit of interest on Twitter.
Search
I have continued to add useful features to the package, including the ability to search Twitter.
<<Twitter`
Column[Take[TwitterSearch["twitter mathematica"], 5], Dividers->All]
TwitterStatus[<netzturbine: ‚ô∫ @imabug cool, mathematica + the twitter API http://bit.ly/1Wv0iV - should work w/ !laconica 2>]
TwitterStatus[<imabug: cool, mathematica and the twitter API http://bit.ly/1Wv0iV>]
TwitterStatus[<kdrewien: RT @PragueBob Wolframs mainstream Mathematica software is plugging into Twitter: http://cli.gs/257htM Geeky!>]
TwitterStatus[<lunajade: How to Twitter with Mathematica and analyze the data... http://bit.ly/14WA8F (via @WolframResearch) [VERY interesting...]>]
TwitterStatus[<pythonism: http://twitter.com/MikeCr/statuses/1835493378 "@ruby_gem Mathematica, firefox, python">]
Adding this functionality was actually a little more difficult than it should have been because the Twitter search API returns a different flavor of XML (ATOM) than the regular Twitter API.
Also, I renamed the HTTP.m package (which was used by Twitter.m) to WebUtils.m and I added some other useful functionality, including the ability to interact with a few popular URL shortening/expanding services. This has enabled some interesting possibilities.
Tweet cache
As you may already know, Wolfram|Alpha launched this past weekend. The website went live on Friday evening and the official launch was Monday afternoon. Sometime Friday afternoon I started running a short Mathematica program that used the TwitterSearch[] function to download all tweets mentioning Wolfram|Alpha and stuff them into an SQLite database. The program is still running, downloading new tweets as they happen.
db = Database`OpenDatabase["Twitter.sqlite"]
Database`Database[Twitter.sqlite]
Database`QueryDatabase[db, "CREATE TABLE tweets (id INTEGER PRIMARY KEY, text TEXT, source TEXT, created_at DATE, in_reply_to_status_id INTEGER, in_reply_to_user_id INTEGER, in_reply_to_screen_name TEXT, user_id INTEGER, user_screen_name TEXT, user_name TEXT, user_profile_image_url TEXT);"];
TwitterStatusDateDBString[status_TwitterStatus] :=
    DateString[TwitterStatusDate[status], {
            "Year", "-", "Month", "-", "Day", " ",
            "Hour", ":", "Minute", ":", "Second"
        }];
InsertTweet[db_Database`Database, status_TwitterStatus]:=Module[{query, user, vals}, query = "INSERT INTO tweets (id, text, source, created_at, in_reply_to_status_id, in_reply_to_user_id, user_screen_name, user_name, user_profile_image_url) values (?, ?, ?, ?, ?, ?, ?, ?, ?)";
    user = TwitterStatusUser[status];
    vals = {
        TwitterStatusID[status],
        TwitterStatusText[status],
        TwitterStatusSource[status],
        TwitterStatusDateDBString[status],
        TwitterStatusReplyID[status],
        TwitterStatusReplyUserID[status],
        TwitterUserScreenName[user],
        TwitterUserName[user],
        TwitterUserProfileImageURL[user]
    };
    Database`QueryDatabase[db, query, vals]
];
query = "wolframalpha OR wolfram_alpha OR \"wolfram alpha\"";
TwitterSearchSince[query_String, id_Integer]:=Module[{tweets = {}, lastCount = - 1, page = 1},
    While[Length[tweets] =!= lastCount,
        lastCount = Length[tweets];
        tweets = Join[tweets,
            TwitterSearch[query, "Results"->100, "Since"->id, "Page"->page++]
        ]
    ];
    tweets
];
since = TwitterStatusID[First[TwitterSearch[query]]];
UpdateCache[]:=While[True,
    tweets = TwitterSearchSince[query, since];
    Monitor[
        Do[InsertTweet[db, tweets[[i]]], {i, Length[tweets]}], ProgressIndicator[Dynamic[i/Length[tweets]]]
    ];
    since = If[Length[tweets]>0, TwitterStatusID[First[tweets]], since];
    Print["added ", ToString[Length[tweets]], " tweets to database at ", DateString[]];
    Pause[30]
];
UpdateCache[]
I chose SQLite because it's easy to use, it's included with Mathematica (though possibly undocumented), it can be accessed easily via a command line tool, and it can be safely accessed by multiple processes at the same time. I started the program five days ago and it's still running. I am able to query the database from a different Mathematica process without interrupting the tweet downloads.
Tweet rate
So, from the other instance of Mathematica I am able to do things like this.
db = Database`OpenDatabase["Twitter.sqlite"]
Database`Database[Twitter.sqlite]
Length[ids = Database`QueryDatabase[db, "select id from tweets"]]
62659
62,659 tweets mentioning Wolfram|Alpha between Friday and Wednesday of launch week. Let's take a look at the timeline. First, grab the creation date of each tweet in the database.
dateStrs = Database`QueryDatabase[db, "select created_at from tweets"];
Convert the strings into Mathematica DateList[] notation.
dates = Monitor[Table[DateList[dateStrs[[i, 1]]], {i, Length[dateStrs]}], ProgressIndicator[Dynamic[i / Length[dateStrs]]]];
Tally the number of tweets per hour.
tally = Tally[{#[[1]], #[[2]], #[[3]], #[[4]], 0, 0}&/@dates];
DateListPlot[tally, Joined->True, FrameLabel->{"Date", "Tweets per hour"}, PlotRange->{{First[dates], DatePlus[DateList[], { - 1, "Hour"}]}, Automatic}, PlotLabel->"Wolfram|Alpha tweet rate", Filling->Axis, ImageSize->{500, Automatic}]
Wolfram|Alpha tweet rate
There are large spikes in tweets per hour around the time the website went live on Friday evening, and again when the site officially launched on Monday.
Tweet links
Since many people post URLs in their tweets it might be interesting to take a look at these to see which web pages and blogs about Wolfram|Alpha are generating the most interest.
tweets = Database`QueryDatabase[db, "select text from tweets"][[All, 1]];
There is a wide variation in the way people post URLs to Twitter, so unfortunately I couldn't find a single regular expression that would find every single one of them. This one works reasonably well.
Length[urls = Flatten[StringCases[#, "http://"~~Except[">"|"]"|"\""|"'"|","|WhitespaceCharacter]..]&/@tweets]]
37565
Length[tally = Tally[urls]]
17969
So there appear to be 37,565 links posted, 17,969 of which are unique. The thing about these URLs is that many use URL shortening services. So it's quite possible many shortened URLs point to the same destination URL. No matter. We can use the URLExpand[] function in my WebUtils package to expand URLs from many of the common URL shortening services.
Unfortunately, that much network traffic takes a long time. So let's cache the results as a list of rules so we can avoid future lookups of the same short URL if possible.
urlMap = {};
expandURL[url_String] := Module[
    {newurl},
    newurl = url /. urlMap;
    If[newurl === url,
        newurl = URLExpand[url];
        If[newurl =!= url, AppendTo[urlMap, url->newurl]];
    ];
    newurl
];
This expansion takes quite some time.
expanded = Monitor[Table[expandURL[urls[[i]]], {i, Length[urls]}], ProgressIndicator[Dynamic[i / Length[urls]]]];
Length[tally = Reverse@SortBy[Tally[expanded], Part[#, 2]&]]
14609
Let's take a look at all of the expanded URLs which were posted more than 100 times.
BarChart[Labeled[Hyperlink[#[[2]], #[[1]]], Rotate[#[[1]], Pi / 2], {Bottom}]&/@Cases[tally, {url_String, n_Integer}/;n>100], ImageSize->{500, Automatic}]
Wolfram|Alpha tweeted URLs
Grid[{#[[2]], Hyperlink[#[[1]]]}&/@Take[tally, 30], Dividers->All, Alignment->{{Right, Left}}]
4475http://www.wolframalpha.com/
1443http://www.wolframalpha.com/screencast/introducingwolframalpha.html
1428http://www.wolframalpha.com
1004http://mashable.com/2009/05/17/wolfram-easter-eggs/
590http://mashable.com/2009/05/19/wolfram-alpha-better-than-google/
528http://mashable.com/2009/05/17/better-wolfram-easter-eggs/
331http://nakedoncam.info/free
316http://www.wolframalpha.com/input/
316http://www.wolframalpha.com/index.html
312http://wolframalpha.com
291http://www.justin.tv/wolframalpha
276http://www.wolfram.com/broadcast/wolframalpha/
201http://justin.tv/wolframalpha
188http://mashable.com/2009/05/15/wolfram-alpha-launch-2/
184http://mashable.com/2009/05/15/wolfram-alpha-video/
173http://www.youtube.com/watch?v=ASnHvwmHuMQ
172http://www.justin.tv/clip/2dd6b9f07e7f8a4e
126http://www.you-got-rick-rolled.com
100http://you-got-rick-rolled.com
97http://www.theregister.co.uk/2009/05/19/dziuba_wolfram/
89http://www.hothotjoboffers.com/32/
87http://business.timesonline.co.uk/tol/business/industry_sectors/technology/article6307744.ece
81http://wolframalpha.com/
72http://www.wolframalpha.com.
71http://lifehacker.com/5257400/first-look-at-wolfram-alphas-impressive-and-fun-knowledge-computation
69http://www.wolframalpha.com/examples/
69http://tedchris.posterous.com/wolfram-alpha-vs-google-1
69http://news.google.com/news/url?sa=T&amp
65http://www.readwriteweb.com/archives/wolfram_alpha_launch_starts_tonight.php
61http://www.wolframalpha.com/input/?i=meaning+of+life
So we have a whole bunch of links directly to the Wolfram|Alpha website, a bunch links to the screencast, a lot of links to some Easter eggs, a porn site (hmmm...), the justin.tv broadcast, Rick-Roll URLs, blog posts, etc. Interesting stuff.
Downloads
Download Twitter.m.
Download WebUtils.m (required by Twitter.m).
Download Mathematica Notebook.
Posted by at 2 comments:
Labels: , , , ,

Tuesday, May 5, 2009

Tri the Illini swim analysis

On Saturday I participated in the Tri the Illini triathlon on the University of Illinois campus. You can read all about the race here. One of the interesting things about this race is that participants were started 10 seconds apart in order of their estimated time for the 300 meter swim in the indoor pool. In theory, if everyone swims at their estimated time nobody will have to pass anyone else in the pool. Now that the results have been posted, let's take a quick look to see how accurate the participants' predictions were.
Import the data from the results web page.
data = Import["http://www.mattoonmultisport.com/images/stories/results/trithetri/overall.htm", {"HTML", "FullData"}];
Clean it up a bit by removing empty elements, labels, and column headers. Basically, we only want the entries with an integer value in the first column (the overall place).
Length[data]
9
data = DeleteCases[data, {}|{{}}];
Length[data]
1
data = First[data];
Length[data]
345
Take[data, 12]//InputForm
{{"", "------- Swim -------", "------- T1 -------",
"------- Bike -------", "------- T2 -------", "------- Run -------",
"Total"}, {"Place", "Name", "Bib No", "Age", "Rnk", "Time", "Pace",
"Rnk", "Time", "Pace", "Rnk", "Time", "Rate", "Rnk", "Time", "Pace",
"Rnk", "Time", "Pace", "Time"}, {1, "Daniel Bretscher", 8, 26, 3,
"04:19.75", "23:59/M", 1, "00:34.00", "", 1, "26:42.95", "24.7mph",
19, "00:44.25", "", 2, "16:09.15", "5:23/M", "48:30.10"},
{2, "Michael Bridenbaug", 27, 25, 15, "04:39.50", "25:50/M", 6,
"00:43.65", "", 5, "28:16.55", "23.3mph", 6, "00:37.55", "", 4,
"16:15.75", "5:25/M", "50:33.00"}, {3, "Peter Garde", 17, 24, 24,
"04:53.05", "27:08/M", 51, "01:21.90", "", 2, "27:06.50", "24.4mph",
109, "01:05.95", "", 3, "16:13.05", "5:24/M", "50:40.45"},
{4, "Nickolaus Early", 16, 29, 2, "04:07.30", "22:52/M", 18,
"00:57.45", "", 4, "27:58.40", "23.6mph", 4, "00:36.40", "", 9,
"18:01.25", "6:00/M", "51:40.80"}, {5, "Zach Rosenbarger", 78, 33, 50,
"05:15.85", "29:10/M", 45, "01:16.75", "", 3, "27:42.00", "23.8mph",
54, "00:53.30", "", 5, "17:11.80", "5:44/M", "52:19.70"},
{6, "Edward Elliot", 32, 28, 11, "04:35.45", "25:28/M", 16, "00:56.15",
"", 6, "28:23.40", "23.3mph", 38, "00:48.85", "", 7, "17:43.75",
"5:54/M", "52:27.60"}, {7, "Ryan Forster", 28, 27, 35, "05:03.95",
"28:03/M", 9, "00:46.20", "", 12, "29:39.95", "22.3mph", 39,
"00:49.05", "", 11, "18:07.00", "6:02/M", "54:26.15"},
{8, "Jun Yamaguchi", 15, 27, 27, "04:58.20", "27:36/M", 2, "00:37.85",
"", 11, "29:36.70", "22.3mph", 30, "00:47.05", "", 13, "18:49.30",
"6:16/M", "54:49.10"}, {9, "Scott Paluska", 63, 42, 71, "05:35.30",
"31:01/M", 3, "00:40.70", "", 7, "28:44.00", "23.0mph", 118,
"01:06.90", "", 12, "18:43.60", "6:14/M", "54:50.50"},
{10, "Rob Raguet-Schoofield", 42, 31, 44, "05:09.75", "28:37/M", 20,
"01:01.55", "", 18, "30:10.50", "21.9mph", 45, "00:51.45", "", 8,
"17:52.60", "5:57/M", "55:05.85"}}
data = DeleteCases[data, x_/;Head[First[x]] === String];
Length[data]
301
places = data[[All, 1]];
places==Range[301]
True
swimSeeds = data[[All, 3]];
swimPlaces = data[[All, 5]];
swimΔ = swimPlaces - swimSeeds;
Take a look at {overall place, swim seed, swim place, swim Δ} for each participant. A negative Δ means the participant's swim place was better than their seeded swim place, while a positive Δ means the participant's swim place was worse than their seeded swim place.
Grid[Prepend[Transpose[{places, swimSeeds, swimPlaces, swimΔ}], {"Overall\nPlace", "Swim\nSeed", "Swim\nPlace", "Swim\nΔ"}], Dividers->All]
Overall
Place		Swim
Seed		Swim
Place		Swim
Δ
183 - 5
22715 - 12
317247
4162 - 14
57850 - 28
63211 - 21
728357
8152712
963718
1042442
11990
126231 - 31
135410551
143014 - 16
15200155 - 45
16148 - 6
1783830
1863327
1947536
206634 - 32
214010262
228610620
2310075 - 25
24455914
2512058 - 62
264128
2733633
283313 - 20
295125 - 26
307211543
3112164
32397 - 32
3365661
34330240 - 90
35486416
36216 - 15
37135 - 8
386856 - 12
3921289 - 123
4021479 - 135
416745 - 22
427621 - 55
4375211136
448163 - 18
45251172 - 79
464411470
4716295 - 67
4874 - 3
49749218
505548 - 7
515229 - 23
52237124 - 113
5311187
54779821
555630 - 26
56117104 - 13
57110
5830074 - 226
59151125 - 26
6013982 - 57
61274151 - 123
626422 - 42
6312287 - 35
6436371
65250243 - 7
66154148 - 6
6712190 - 31
68136258122
69282146 - 136
708769 - 18
71112110 - 2
72315278 - 37
732419 - 5
748077 - 3
7513518449
76699728
77185163 - 22
785949 - 10
7912894 - 34
806051 - 9
8118728 - 159
823520 - 15
8311313421
849040 - 50
8516317 - 146
86223816
8713320067
8826773 - 194
89256145 - 111
909212230
9115920647
92165130 - 35
9313715316
94149128 - 21
9510480 - 24
96182136 - 46
97264620
9817293 - 79
9924155 - 186
100277109 - 168
10111416551
102971036
10313115928
104228194 - 34
1054611771
10614119958
10713216230
108246132 - 114
10911520590
110213183 - 30
11112718154
112157147 - 10
113254131 - 123
114266256 - 10
115416120
1166139 - 22
1174341 - 2
1181911965
119106257151
1209681 - 15
12123460 - 174
12220185 - 116
12310814234
12416121857
12512314926
1269815052
127138271133
128265179 - 86
12919554 - 141
130508636
13153161108
132170137 - 33
1335826 - 32
134169120 - 49
13520424945
13634265 - 277
137911009
13810347 - 56
13912518257
1408268 - 14
1418876 - 12
14214724194
143238107 - 131
144303202 - 101
14570191121
146297247 - 50
147188178 - 10
1482108
14913016434
150311288 - 23
15116818719
152283158 - 125
15314421672
154295287 - 8
15520824436
156287157 - 130
15711117665
158199111 - 88
159272223 - 49
16017924263
16184190106
162310152 - 158
1631091189
164376730
16518022747
166340135 - 205
167328193 - 135
168263197 - 66
169312250 - 62
170148143 - 5
171242224 - 18
172278230 - 48
173253139 - 114
174292279 - 13
175103222
176276254 - 22
1771810183
17815516712
1792712765
18010216967
18119224856
18225778 - 179
18393210117
184346294 - 52
18525526914
18615819234
18749171122
18812620175
189143140 - 3
19023188 - 143
191220186 - 34
192298177 - 121
19310714437
1949412935
19512918859
19618427490
197116273157
19822425935
19918621428
20017419824
201290221 - 69
2029517580
20315221563
20418924657
20515623983
206336141 - 195
20711817456
20819791 - 106
20919428086
21019621216
211291121 - 170
212190189 - 1
213247119 - 128
214286126 - 160
21521952 - 167
216229170 - 59
21723230
21823627741
21923526530
220252204 - 48
22125828123
2229984 - 15
22321122615
224279272 - 7
22521626751
226167116 - 51
22724327532
228262220 - 42
229230154 - 76
230288166 - 122
231337251 - 86
232269228 - 41
23323325219
23420208188
23511018575
236308284 - 24
237261231 - 30
238245127 - 118
239343283 - 60
24016070 - 90
241150264114
2428515671
2435173168
244347213 - 134
24515320350
24617521944
247339298 - 41
248134290156
24920342 - 161
250348282 - 66
251289112 - 177
25212416844
25321823820
25414520762
255119113 - 6
256183123 - 60
257299236 - 63
2587362 - 11
259302261 - 41
260299667
26157570
26217322552
263281255 - 26
264319968
265275270 - 5
266319296 - 23
26718124564
268178301123
2698910819
270307291 - 16
271294229 - 65
27221543 - 172
273176160 - 16
274270180 - 90
275240195 - 45
27621726346
277318302 - 16
278316303 - 13
279285237 - 48
28028029717
28117772 - 105
28220723427
283314217 - 97
284309232 - 77
285306253 - 53
28624829244
28719328996
288296286 - 10
28922728558
29017122251
291345304 - 41
292305262 - 43
29371268197
2942642662
2952262359
296225209 - 16
29727329522
29824426016
299142305163
30020930697
301313307 - 6
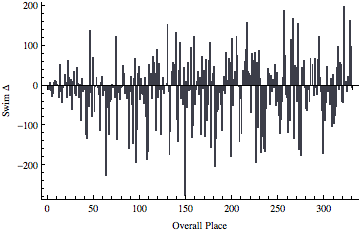
It looks like the race leaders were fairly accurate in their predictions, while the differences start to become greater around 40th place or so.
BarChart[swimΔ, FrameLabel->{"Overall Place", "Swim Δ"}, Frame->{True, True, False, False}]
2009-05-05-TriTheIllini1
From the sorted Δs it looks like about half of the participants were within 50 places or so of their seeds, while a few were way off (in both directions).
BarChart[Sort[swimΔ]]
2009-05-05-TriTheIllini2
Median[Abs@swimΔ]
41
N[Mean[Abs@swimΔ]]
56.70099667774086`
N[StandardDeviation[Abs@swimΔ]]
51.80100030247153`
Commonest[Abs@swimΔ]
{16}
tally = Sort[Tally[Abs@swimΔ]]
{{0, 5}, {1, 3}, {2, 4}, {3, 3}, {4, 1}, {5, 6}, {6, 6}, {7, 6}, {8, 5}, {9, 4}, {10, 5}, {11, 1}, {12, 5}, {13, 3}, {14, 4}, {15, 5}, {16, 10}, {17, 1}, {18, 4}, {19, 3}, {20, 5}, {21, 4}, {22, 6}, {23, 4}, {24, 3}, {25, 1}, {26, 5}, {27, 2}, {28, 4}, {30, 6}, {31, 2}, {32, 4}, {33, 2}, {34, 6}, {35, 4}, {36, 2}, {37, 2}, {41, 5}, {42, 2}, {43, 2}, {44, 3}, {45, 3}, {46, 2}, {47, 2}, {48, 3}, {49, 3}, {50, 3}, {51, 5}, {52, 3}, {53, 1}, {54, 1}, {55, 1}, {56, 3}, {57, 4}, {58, 2}, {59, 2}, {60, 2}, {62, 4}, {63, 3}, {64, 1}, {65, 2}, {66, 2}, {67, 4}, {68, 1}, {69, 1}, {70, 1}, {71, 2}, {72, 1}, {75, 2}, {76, 1}, {77, 1}, {79, 2}, {80, 1}, {83, 2}, {86, 3}, {88, 1}, {90, 5}, {94, 1}, {96, 1}, {97, 2}, {101, 1}, {105, 1}, {106, 2}, {108, 1}, {111, 1}, {113, 1}, {114, 3}, {116, 1}, {117, 1}, {118, 1}, {121, 2}, {122, 3}, {123, 4}, {125, 1}, {128, 1}, {130, 1}, {131, 1}, {133, 1}, {134, 1}, {135, 2}, {136, 2}, {141, 1}, {143, 1}, {146, 1}, {151, 1}, {156, 1}, {157, 1}, {158, 1}, {159, 1}, {160, 1}, {161, 1}, {163, 1}, {167, 1}, {168, 2}, {170, 1}, {172, 1}, {174, 1}, {177, 1}, {179, 1}, {186, 1}, {188, 1}, {194, 1}, {195, 1}, {197, 1}, {205, 1}, {226, 1}, {277, 1}}
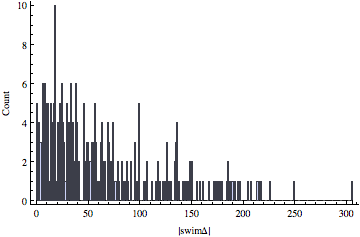
BarChart[Range[0, Max[tally[[All, 1]]]]/.Append[Apply[Rule, tally, 1], _Integer->0], FrameLabel->{TraditionalForm[Abs["swimΔ"]], "Count"}, Frame->{True, True, False, False}]
2009-05-05-TriTheIllini3
It looks like most people were 40-50 places off (in one direction or the other) from their seed. This is higher than I would have expected. The most common difference was 16 places. There must have been a lot of passing going on.
Download Mathematica Notebook
Posted by at 2 comments:
Labels: , ,
Subscribe to: Posts (Atom)